S26L02 – भ्रम तालिका

html
मशीन लर्निंग में भ्रम मैट्रिक्स को समझना: एक व्यापक मार्गदर्शिका

विषय सूची

    भ्रम मैट्रिक्स क्या है?
    मुख्य घटकों की व्याख्या
    मॉडल मूल्यांकन में भ्रम मैट्रिक्स का महत्व
    त्रुटि प्रकारों के आधार पर सही मॉडल का चयन
    मल्टी-क्लास भ्रम मैट्रिक्स
    Scikit-learn के साथ भ्रम मैट्रिक्स का दृश्यीकरण
    भ्रम मैट्रिक्स के उपयोग के फायदे
    संभावित बाधाएँ
    सर्वश्रेष्ठ प्रथाएँ
    निष्कर्ष


भ्रम मैट्रिक्स क्या है?
एक भ्रम मैट्रिक्स एक सारणीबद्ध प्रस्तुति है जो आपको एक श्रेणीबद्धण एल्गोरिथ्म के प्रदर्शन को दृश्यीकृत करने की अनुमति देती है। भविष्यवाणी किए गए परिणामों की तुलना वास्तविक परिणामों से करके, यह मॉडल द्वारा की गई त्रुटियों के प्रकारों में स्पष्ट अंतर्दृष्टि प्रदान करता है। यह मैट्रिक्स विशेष रूप से द्विआधारी और बहु-श्रेणीबद्धण समस्याओं में उपयोगी है।

भ्रम मैट्रिक्स का ढांचा
एक द्विआधारी श्रेणीबद्धण समस्या के लिए, भ्रम मैट्रिक्स एक 2x2 तालिका होती है, जबकि बहु-श्रेणीबद्धण के लिए, यह NxN मैट्रिक्स तक विस्तारित हो जाती है, जहाँ N श्रेणियों की संख्या को दर्शाता है।


छवि स्रोत: Scikit-learn भ्रम मैट्रिक्स उदाहरण

मैट्रिक्स में निम्नलिखित घटक शामिल हैं:


    
        
        भविष्यवाणी सकारात्मक (P)
        भविष्यवाणी नकारात्मक (N)
    
    
        वास्तविक सकारात्मक (P)
        सच्चा सकारात्मक (TP)
        फ्रॉज नकारात्मक (FN)
    
    
        वास्तविक नकारात्मक (N)
        फ्रॉज सकारात्मक (FP)
        सच्चा नकारात्मक (TN)
    


मुख्य घटकों की व्याख्या

सच्चा सकारात्मक (TP)

    परिभाषा: मॉडल सही ढंग से सकारात्मक वर्ग की भविष्यवाणी करता है।
    उदाहरण: यह भविष्यवाणी करना कि ईमेल स्पैम है, और वास्तव में वह स्पैम होना।


सच्चा नकारात्मक (TN)

    परिभाषा: मॉडल सही ढंग से नकारात्मक वर्ग की भविष्यवाणी करता है।
    उदाहरण: यह भविष्यवाणी करना कि ईमेल स्पैम नहीं है, और वास्तव में वह स्पैम नहीं होना।


फ्रॉज सकारात्मक (FP) – प्रकार I त्रुटि

    परिभाषा: मॉडल गलत तरीके से सकारात्मक वर्ग की भविष्यवाणी करता है।
    भी जाना जाता है: प्रकार I त्रुटि।
    उदाहरण: यह भविष्यवाणी करना कि ईमेल स्पैम है, लेकिन वास्तव में वह स्पैम नहीं होना।
    प्रभाव: संदर्भ के अनुसार, प्रकार I त्रुटियाँ कम महत्वपूर्ण हो सकती हैं, जैसे कि एक वैध ईमेल को गलत तरीके से स्पैम के रूप में चिह्नित करना।


फ्रॉज नकारात्मक (FN) – प्रकार II त्रुटि

    परिभाषा: मॉडल गलत तरीके से नकारात्मक वर्ग की भविष्यवाणी करता है।
    भी जाना जाता है: प्रकार II त्रुटि।
    उदाहरण: यह भविष्यवाणी करना कि ईमेल स्पैम नहीं है, लेकिन वास्तव में वह स्पैम होना।
    प्रभाव: चिकित्सा निदान जैसे महत्वपूर्ण अनुप्रयोगों में, प्रकार II त्रुटियाँ खतरनाक हो सकती हैं, जैसे कि कैंसर को होने पर नहीं पहचान पाना।


मॉडल मूल्यांकन में भ्रम मैट्रिक्स का महत्व
भ्रम मैट्रिक्स कई मूल्यांकन मेट्रिक्स के लिए आधार है, जिनमें शामिल हैं:


    सटीकता (Accuracy): (TP + TN) / (TP + TN + FP + FN)
    प्रिसिजन (Precision): TP / (TP + FP)
    रिकॉल (सेंसिटिविटी): TP / (TP + FN)
    F1 स्कोर: 2 * (प्रिसिजन * रिकॉल) / (प्रिसिजन + रिकॉल)


ये मेट्रिक्स केवल सटीकता से परे मॉडल के प्रदर्शन की सूक्ष्म समझ प्रदान करते हैं, विशेष रूप से उन परिदृश्यों में जहाँ डेटा असंतुलित होता है।

त्रुटि प्रकारों के आधार पर सही मॉडल का चयन
विभिन्न अनुप्रयोग विभिन्न प्रकार की त्रुटियों को कम करने पर जोर देते हैं:


    चिकित्सा निदान: प्रकार II त्रुटियों को कम करने को प्राथमिकता देना ताकि कैंसर जैसी स्थितियों को न चूका जाए।
    स्पैम डिटेक्शन: प्रकार I त्रुटियों को कम करने से वैध ईमेल को अनावश्यक रूप से स्पैम के रूप में चिह्नित होने से रोका जा सकता है।


उदाहरण के लिए, सपोर्ट वेक्टर मशीन (SVM) जैसे मॉडल तब पसंद किए जाते हैं जब प्रकार II त्रुटियों को कम करना महत्वपूर्ण होता है, जबकि XGBoost ऐसे परिदृश्यों के लिए चुना जा सकता है जहाँ प्रकार I त्रुटियाँ अधिक महत्वपूर्ण होती हैं।

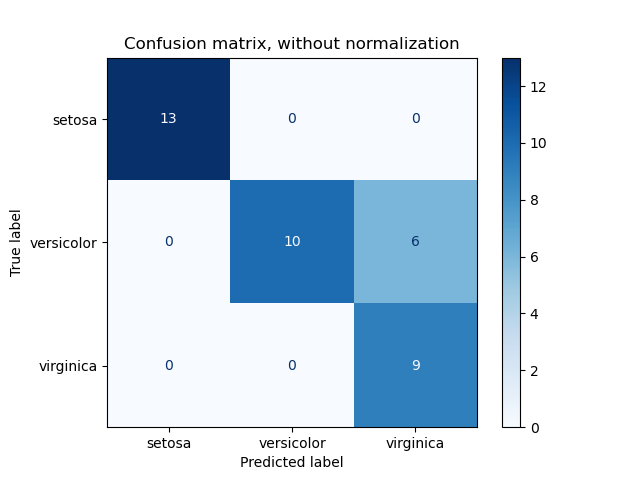
मल्टी-क्लास भ्रम मैट्रिक्स
जहाँ द्विआधारी वर्गीकरण सरल होता है, वहीं बहु-श्रेणीबद्धण जटिलता पेश करता है। ऐसे मामलों में, भ्रम मैट्रिक्स सभी श्रेणियों को समायोजित करने के लिए विस्तारित हो जाता है, जिसमें प्रत्येक पंक्ति वास्तविक श्रेणी और प्रत्येक स्तंभ भविष्यवाणी की गई श्रेणी को दर्शाता है।

आयरीज़ डेटासेट के साथ उदाहरण
आयरीज़ डेटासेट पर विचार करें, जिसमें तीन श्रेणियाँ शामिल हैं: सेटोसा, वर्सिकोलर, और वर्जीनिका। एक मल्टी-क्लास श्रेणीबद्धण मॉडल के लिए भ्रम मैट्रिक्स इस प्रकार दिख सकता है:


    
        
        सेटोसा
        वर्सिकोलर
        वर्जीनिका
    
    
        सेटोसा
        12
        0
        0
    
    
        वर्सिकोलर
        1
        10
        1
    
    
        वर्जीनिका
        0
        2
        12
    


यह मैट्रिक्स प्रत्येक श्रेणी के लिए सही और गलत भविष्यवाणियों की संख्या को दर्शाता है, जिससे एक विस्तृत प्रदर्शन मूल्यांकन में आसानी होती है।

Scikit-learn के साथ भ्रम मैट्रिक्स का दृश्यीकरण
पायथन की Scikit-learn पुस्तकालय में भ्रम मैट्रिक्स को प्लॉट और विश्लेषण करने के लिए अंतर्निर्मित फंक्शन्स हैं, जो व्याख्यात्मकता बढ़ाते हैं।

भ्रम मैट्रिक्स प्लॉट करने के लिए सैंपल कोड




		
		
			
			
Java
			
			from sklearn.metrics import confusion_matrix, plot_confusion_matrix
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.datasets import load_iris

# Load dataset
iris = load_iris()
X = iris.data
y = iris.target

# Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# Initialize and train the model
model = SVC(kernel='linear', C=0.01).fit(X_train, y_train)

# Plot confusion matrix
plot_confusion_matrix(model, X_test, y_test, display_labels=iris.target_names, cmap=plt.cm.Blues, normalize='true')
plt.title('Confusion Matrix - Iris Dataset')
plt.show()
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
				
						from sklearn.metrics import confusion_matrix, plot_confusion_matrix
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.datasets import load_iris
 
# Load dataset
iris = load_iris()
X = iris.data
y = iris.target
 
# Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
 
# Initialize and train the model
model = SVC(kernel='linear', C=0.01).fit(X_train, y_train)
 
# Plot confusion matrix
plot_confusion_matrix(model, X_test, y_test, display_labels=iris.target_names, cmap=plt.cm.Blues, normalize='true')
plt.title('Confusion Matrix - Iris Dataset')
plt.show()
					
				
			
		


यह कोड स्निपेट आयरीज़ डेटासेट पर एक SVM मॉडल को प्रशिक्षित करता है और सामान्यीकृत भ्रम मैट्रिक्स को दृश्यीकृत करता है, जिससे विभिन्न श्रेणियों में मॉडल के प्रदर्शन की स्पष्ट अंतर्दृष्टि मिलती है।

भ्रम मैट्रिक्स के उपयोग के फायदे

    विस्तृत त्रुटि विश्लेषण: त्रुटियों के विशिष्ट प्रकारों की पहचान करता है, लक्षित सुधारों को सुगम बनाता है।
    मॉडल तुलना: उनके त्रुटि प्रोफाइल के आधार पर विभिन्न मॉडलों की तुलना करने में सक्षम बनाता है।
    असंतुलित डेटा को संभालना: विभिन्न श्रेणियों में मॉडलों के प्रदर्शन पर स्पष्टता प्रदान करता है, विशेष रूप से असंतुलित डेटासेट में।


संभावित बाधाएँ

    कई श्रेणियों के साथ जटिलता: जैसे-जैसे श्रेणियों की संख्या बढ़ती है, भ्रम मैट्रिक्स बड़ा और समझने में कठिन हो सकता है।
    गुमराह करने वाली सटीकता: असंतुलित डेटासेट में, उच्च सटीकता धोखा दे सकती है। भ्रम मैट्रिक्स ऐसे प्रदर्शन मुद्दों को उजागर करने में मदद करता है जिन्हें केवल सटीकता छुपा सकती है।


सर्वश्रेष्ठ प्रथाएँ

    मैट्रिक्स को सामान्यीकृत करें: विशेष रूप से मल्टी-क्लास परिदृश्यों में सही और गलत भविष्यवाणियों के अनुपात को समझने के लिए उपयोगी।
    अन्य मेट्रिक्स के साथ संयोजन करें: समग्र मूल्यांकन के लिए प्रिसिजन, रिकॉल, और F1 स्कोर के साथ उपयोग करें।
    दृश्य प्रतिनिधित्व: मैट्रिक्स में पैटर्नों को अधिक स्पष्ट रूप से पहचानने के लिए रंग ग्रेडिएंट्स का उपयोग करें।


निष्कर्ष
भ्रम मैट्रिक्स मशीन लर्निंग टूलकिट में एक अनिवार्य उपकरण है, जो श्रेणीबद्धण मॉडलों के आंतरिक कार्यों में एक विंडो की तरह काम करता है। इसके घटकों को समझकर और इसकी अंतर्दृष्टियों का उपयोग करके, डेटा वैज्ञानिक मॉडल के प्रदर्शन को बेहतर बनाने, उपयुक्त एल्गोरिदम का चयन करने, और महत्वपूर्ण त्रुटियों को कम करने के लिए सूचित निर्णय ले सकते हैं। जैसे-जैसे मशीन लर्निंग का विकास जारी रहेगा, भ्रम मैट्रिक्स में महारत हासिल करना प्रभावी मॉडल मूल्यांकन और कार्यान्वयन की नींव बना रहेगा।



अधिक पढ़ें:

    Scikit-learn भ्रम मैट्रिक्स दस्तावेज़
    प्रिसिजन और रिकॉल को समझना


अपडेट रहना जारी रखें:
मशीन लर्निंग मूल्यांकन तकनीकों में और अधिक अंतर्दृष्टि के लिए, हमारे न्यूज़लेटर को सब्सक्राइब करें और हमारे ब्लॉग अपडेट का अनुसरण करें।
	सेटोसा	वर्सिकोलर	वर्जीनिका
सेटोसा	12	0	0
वर्सिकोलर	1	10	1
वर्जीनिका	0	2	12
	भविष्यवाणी सकारात्मक (P)	भविष्यवाणी नकारात्मक (N)
वास्तविक सकारात्मक (P)	सच्चा सकारात्मक (TP)	फ्रॉज नकारात्मक (FN)
वास्तविक नकारात्मक (N)	फ्रॉज सकारात्मक (FP)	सच्चा नकारात्मक (TN)