S26L03 – सटीकता, शुद्धता, पुनः प्राप्ति, विशिष्टता, एफ1 स्कोर

html
मॉडल मूल्यांकन में सटीकता, प्रेसिजन, रिकॉल, विशिष्टता और F1 स्कोर को समझना

सामग्री तालिका

    मॉडल मूल्यांकन मीट्रिक का परिचय
    कन्फ्यूजन मैट्रिक्स: आधार
    सटीकता: प्रारंभिक बिंदु
    प्रेसिजन: सटीकता मापन
    रिकॉल (संवेदनशीलता): पूर्णता मापन
    विशिष्टता: कम आंका गया मीट्रिक
    F1 स्कोर: प्रेसिजन और रिकॉल का संतुलन
    अपने मॉडल के लिए सही मीट्रिक चुनना
    मेट्रिक गणना के लिए Scikit-Learn का उपयोग
    निष्कर्ष


मॉडल मूल्यांकन मीट्रिक का परिचय
जब आप वर्गीकरण मॉडल विकसित कर रहे होते हैं, तो यह मूल्यांकन करना महत्वपूर्ण होता है कि आपका मॉडल केवल समग्र सटीकता से परे कितना अच्छा प्रदर्शन करता है। विभिन्न मीट्रिक आपके मॉडल के प्रदर्शन के विभिन्न पहलुओं पर अंतर्दृष्टि प्रदान करते हैं, जिससे आप अपने अनुप्रयोग की विशिष्ट आवश्यकताओं के आधार पर सूचित निर्णय ले सकते हैं।

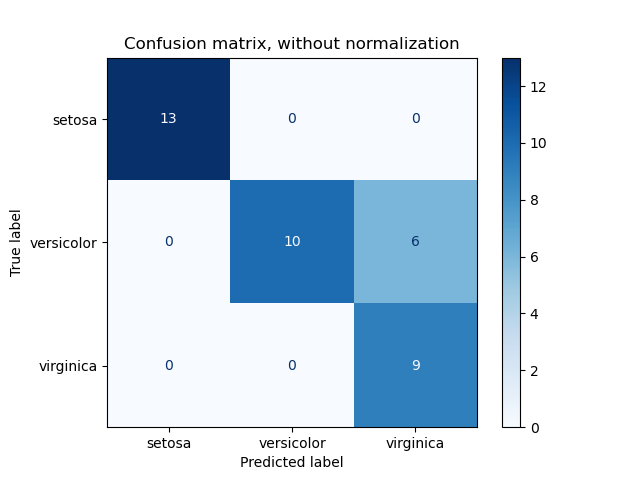
कन्फ्यूजन मैट्रिक्स: आधार
कन्फ्यूजन मैट्रिक्स एक तालिका होती है जो वर्गीकरण मॉडल के प्रदर्शन का विज़ुअलाइज़ेशन करने की अनुमति देती है। यह वास्तविक लक्ष्यों के मान की तुलना मॉडल द्वारा भविष्यवाणी किए गए मानों से करती है। बाइनरी वर्गीकरण के लिए, कन्फ्यूजन मैट्रिक्स एक 2x2 मैट्रिक्स होता है जिसमें शामिल होते हैं:

    True Positives (TP): सही ढंग से भविष्यवाणी की गई सकारात्मक उदाहरण।
    False Positives (FP): गलत ढंग से भविष्यवाणी की गई सकारात्मक उदाहरण।
    True Negatives (TN): सही ढंग से भविष्यवाणी की गई नकारात्मक उदाहरण।
    False Negatives (FN): गलत ढंग से भविष्यवाणी की गई नकारात्मक उदाहरण।


इन घटकों को समझना आवश्यक है क्योंकि ये विभिन्न प्रदर्शन मीट्रिक की गणना के आधार के रूप में काम करते हैं।

सटीकता: प्रारंभिक बिंदु
सटीकता सबसे सरल मीट्रिक है, जो कुल सही भविष्यवाणियों का प्रतिशत प्रदर्शित करती है, सभी किए गए भविष्यवाणियों में से।

सूत्र:
\[ \text{Accuracy} = \frac{TP + TN}{TP + FP + FN + TN} \]

उदाहरण:
एक परिदृश्य पर विचार करें जहाँ एक मॉडल 10 ट्रू पॉजिटिव्स, 9 ट्रू नेगेटिव्स को भविष्यवाणी करता है, और कुछ गलत भविष्यवाणियाँ हैं:
\[ \text{Accuracy} = \frac{10 + 9}{10 + 9 + 0 + 0} = 97.5\% \]
जबकि 97.5% की सटीकता प्रभावशाली लगती है, इसकी सीमाओं को पहचानना आवश्यक है, विशेष रूप से असंतुलित डेटासेट के मामलों में जहाँ एक वर्ग दूसरे से काफी अधिक है।

प्रेसिजन: सटीकता मापन
प्रेसिजन यह आकलन करता है कि कितने सकारात्मक भविष्यवाणी किए गए उदाहरण वास्तव में सही हैं। यह प्रश्न का उत्तर देता है: जब मॉडल एक सकारात्मक वर्ग की भविष्यवाणी करता है, तो कितनी बार वह सही होता है?

सूत्र:
\[ \text{Precision} = \frac{TP}{TP + FP} \]

उदाहरण:
उसी मॉडल का उपयोग करते हुए:
\[ \text{Precision} = \frac{10}{10 + 250} = 3.8\% \]
कम प्रेसिजन उच्च संख्या में फॉल्स पॉजिटिव्स को दर्शाता है, जो ऐसे अनुप्रयोगों में समस्याजनक हो सकता है जहाँ फेल्स अलार्म महंगी होती हैं।

प्रेसिजन का महत्व:
प्रेसिजन ऐसे परिदृश्यों में महत्वपूर्ण है जहाँ फॉल्स पॉजिटिव्स की लागत उच्च होती है, जैसे स्पेम डिटेक्शन या मेडिकल डायग्नोस्टिक्स।

रिकॉल (संवेदनशीलता): पूर्णता मापन
रिकॉल, जिसे संवेदनशीलता भी कहा जाता है, यह मापता है कि मॉडल सभी प्रासंगिक उदाहरणों की पहचान करने में कितना सक्षम है। यह प्रश्न का उत्तर देता है: सभी वास्तविक सकारात्मक उदाहरणों में से, मॉडल ने कितने सही ढंग से पहचान किए?

सूत्र:
\[ \text{Recall} = \frac{TP}{TP + FN} \]

उदाहरण:
\[ \text{Recall} = \frac{10}{10 + 5} = 66.6\% \]
उच्च रिकॉल यह दर्शाता है कि मॉडल सकारात्मक वर्ग का एक बड़ा हिस्सा पकड़ रहा है, जो रोग स्क्रीनिंग जैसी अनुप्रयोगों में वांछनीय है।

रिकॉल का महत्व:
रिकॉल ऐसी परिस्थितियों में महत्वपूर्ण है जहाँ एक सकारात्मक उदाहरण को मिस करना गंभीर परिणाम रखता है, जैसे रोग पहचान या सुरक्षा खतरे की पहचान में।

विशिष्टता: कम आंका गया मीट्रिक
विशिष्टता वास्तविक नकारात्मकों के हिस्से को मापती है जो सही ढंग से पहचाने गए हैं। यह प्रश्न का उत्तर देती है: सभी वास्तविक नकारात्मक उदाहरणों में से, मॉडल ने कितने सही ढंग से पहचाना?

सूत्र:
\[ \text{Specificity} = \frac{TN}{TN + FP} \]

उदाहरण:
\[ \text{Specificity} = \frac{9990}{9990 + 250} = 97.55\% \]
उच्च विशिष्टता यह इंगित करती है कि मॉडल नकारात्मक उदाहरणों की पहचान में प्रभावी है, जो ऐसी परिस्थितियों में महत्वपूर्ण है जहाँ फॉल्स नेगेटिव्स विशेष रूप से अवांछनीय होते हैं।

विशिष्टता का महत्व:
विशिष्टता ऐसे अनुप्रयोगों में आवश्यक है जहाँ नकारात्मक वर्ग की सटीक पहचान महत्वपूर्ण होती है, जैसे धोखाधड़ी पहचान या गैर-रोग (स्वस्थ) वर्गीकरण।

F1 स्कोर: प्रेसिजन और रिकॉल का संतुलन
F1 स्कोर प्रेसिजन और रिकॉल का हार्मोनिक माध्य है, जो दोनों चिंताओं को संतुलित करने वाला एकल मीट्रिक प्रदान करता है। अंकगणितीय माध्य के विपरीत, F1 स्कोर प्रेसिजन और रिकॉल के बीच के व्यापार को ध्यान में रखता है।

सूत्र:
\[ \text{F1 Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]

उदाहरण:
\[ \text{F1 Score} = 2 \times \frac{0.038 \times 0.666}{0.038 + 0.666} \approx 7.1\% \]
F1 स्कोर विशेष रूप से उपयोगी है जब आपको प्रेसिजन और रिकॉल के बीच संतुलन की आवश्यकता होती है और जब वर्ग वितरण असमान होता है।

F1 स्कोर का महत्व:
F1 स्कोर उन परिस्थितियों के लिए आदर्श है जहाँ फॉल्स पॉजिटिव्स और फॉल्स नेगेटिव्स दोनों को न्यूनतम करना महत्वपूर्ण होता है, जिससे मॉडल के प्रदर्शन की अधिक सूक्ष्म दृष्टि मिलती है।

अपने मॉडल के लिए सही मीट्रिक चुनना
उपयुक्त मूल्यांकन मीट्रिक का चयन आपके प्रोजेक्ट की विशिष्ट आवश्यकताओं और संदर्भ पर निर्भर करता है:

    सटीकता का उपयोग करें जब वर्ग संतुलित हों और सभी त्रुटियाँ समान रूप से कीमती हों।
    प्रेसिजन का उपयोग करें जब फॉल्स पॉजिटिव्स की लागत उच्च हो।
    रिकॉल का उपयोग करें जब फॉल्स नेगेटिव्स की लागत उच्च हो।
    विशिष्टता का उपयोग करें जब नकारात्मक वर्ग की सही पहचान महत्वपूर्ण हो।
    F1 स्कोर का उपयोग करें जब आपको प्रेसिजन और रिकॉल के बीच संतुलन की आवश्यकता हो, विशेषकर असंतुलित डेटासेट में।

इन मीट्रिक को समझना यह सुनिश्चित करता है कि आप अपने प्रोजेक्ट के लक्ष्यों और प्रतिबंधों के अनुरूप सही मीट्रिक का चयन करें।

मेट्रिक गणना के लिए Scikit-Learn का उपयोग
इन मीट्रिक को मैन्युअल रूप से गणना करना थकाऊ और त्रुटिपूर्ण हो सकता है, खासकर अधिक जटिल मॉडलों के लिए। सौभाग्य से, Python की Scikit-Learn लाइब्रेरी इन मीट्रिक की सहज रूप से गणना करने के लिए मजबूत उपकरण प्रदान करती है।

उपयोगी Scikit-Learn फ़ंक्शंस:

accuracy_score: सटीकता की गणना करता है।

precision_score: प्रेसिजन की गणना करता है।

recall_score: रिकॉल की गणना करता है।

f1_score: F1 स्कोर की गणना करता है।

confusion_matrix: कन्फ्यूजन मैट्रिक्स उत्पन्न करता है।

classification_report: ऊपर के सभी मीट्रिक सहित विस्तृत रिपोर्ट प्रदान करता है।



उदाहरण:




		
		
			
			
Java
			
			from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score

# Assume y_true and y_pred are your actual and predicted labels
conf_matrix = confusion_matrix(y_true, y_pred)
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)

print("Confusion Matrix:\n", conf_matrix)
print(f"Accuracy: {accuracy * 100:.2f}%")
print(f"Precision: {precision * 100:.2f}%")
print(f"Recall: {recall * 100:.2f}%")
print(f"F1 Score: {f1 * 100:.2f}%")
			
				
					
				
					1
2
3
4
5
6
7
8
9
10
11
12
13
14
				
						from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
 
# Assume y_true and y_pred are your actual and predicted labels
conf_matrix = confusion_matrix(y_true, y_pred)
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
 
print("Confusion Matrix:\n", conf_matrix)
print(f"Accuracy: {accuracy * 100:.2f}%")
print(f"Precision: {precision * 100:.2f}%")
print(f"Recall: {recall * 100:.2f}%")
print(f"F1 Score: {f1 * 100:.2f}%")
					
				
			
		



और अधिक उन्नत मीट्रिक गणनाओं के लिए, जिसमें विशिष्टता शामिल है, आप classification_report का उपयोग कर सकते हैं या अतिरिक्त Scikit-Learn संसाधनों का अन्वेषण कर सकते हैं:

    Scikit-Learn Classification Report
    Scikit-Learn Model Evaluation


निष्कर्ष
एक वर्गीकरण मॉडल के प्रदर्शन का मूल्यांकन महज सटीकता से आगे बढ़ कर एक सूक्ष्म दृष्टिकोण की आवश्यकता होती है। प्रेसिजन, रिकॉल, विशिष्टता और F1 स्कोर जैसे मीट्रिक को समझकर और उनका उपयोग करके, आप अपने मॉडल की ताकत और कमजोरियों पर गहरी अंतर्दृष्टि प्राप्त करते हैं। यह व्यापक मूल्यांकन सुनिश्चित करता है कि आपका मॉडल वास्तविक दुनिया के परिदृश्यों में उत्तम प्रदर्शन करता है, आपके प्रोजेक्ट के विशिष्ट लक्ष्यों और आवश्यकताओं के अनुरूप।
याद रखें, मीट्रिक का चयन हमेशा आपके अनुप्रयोग के संदर्भ द्वारा निर्देशित होना चाहिए। Scikit-Learn जैसे उपकरणों का उपयोग करके इस प्रक्रिया को सुव्यवस्थित करें, जिससे आप सर्वोत्तम संभव परिणामों के लिए अपने मॉडलों को परिष्कृत करने पर ध्यान केंद्रित कर सकें।



Keywords: सटीकता, प्रेसिजन, रिकॉल, विशिष्टता, F1 स्कोर, कन्फ्यूजन मैट्रिक्स, मॉडल मूल्यांकन, मशीन लर्निंग मीट्रिक, Scikit-Learn, वर्गीकरण मॉडल प्रदर्शन।